A Study on Steady Solutions of Nonlinear Wave
[How material is made from light]
[How did I
get to 11 dimensional standing wave solution]
By recent experiments of
high-energy accelerator it has already confirmed that eMaterial could be
developed by collision of lightsf.
From this matter we can
guess that eAll materials is made of lightf, but it hasnft confirmed.
I propose an idea here that
eMaterial could be formed by the nonlinear electromagnetic wave as a phenomenon
of self-organizationf.
Of course eelectromagnetic
wavef means lights.
It is known that the espeed
of light in matterf depends on the strength of the electromagnetic waves and it
causes variety of non-linear effects.
Rectifier circuit is using
nonlinearity of electronic devices.
I thoughts electromagnetic AC(alternating current)waves converts electromagnetic
DC(direct current ) waves.
A kind of
"rectification could be
happened by it's nonlinearity in the matter.
Then I tried simulation such
as the following.
Please browse 'nonlinear
wave 1-dimensional animation'.
E_AC is AC electric field
that has short wavelength.
E_DC is DC electric field
that has long wavelength.
AC and DC electric fields
are mixed.
AC electric field progresses
from left to right.
DC electric field does not
proceed. The initial value of the changing rate is 0.
The speed of light is
normalizes to 1.
When the strength of
electric field exceeds the constants E1, the speed of light decreases ’c(0.005).
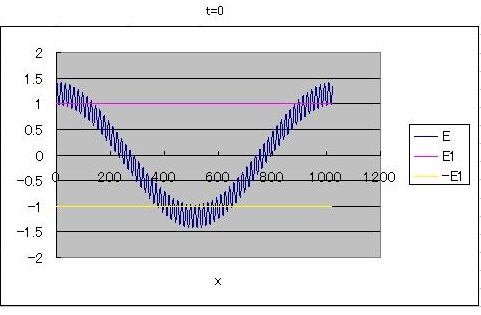
According to Maxwell's
equations I simulated using difference method.
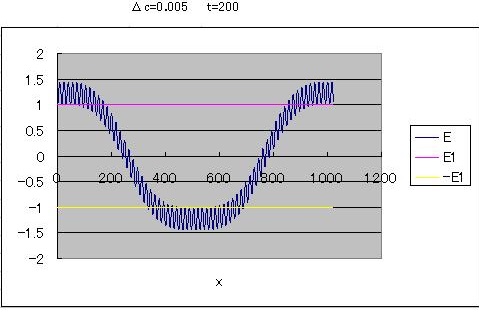
"Rectification" is
now maintained by the nonlinearity of DC electric field.
This is a phenomenon of
self-organization.
Up to here the situation is
in material.
But how about in vacuum
space.
Generally, speed of light in
a vacuum is considered constant.
But even if very strong
electromagnetic fields, is speed of light really constant?
In the immediate near of
proton or electron, electromagnetic field is very strong, who can measure the
linearity in such situations?
I extended to a
three-dimensional situation from Above-mentioned one-dimensional situation.
I seek E_DC Laplacian of Gaussian noise in the steady state.
Please see
A related expression of the three-dimensional steady solution
of the non-linear wave equation
E_DC Laplacian
is derived as a function of E_DC,
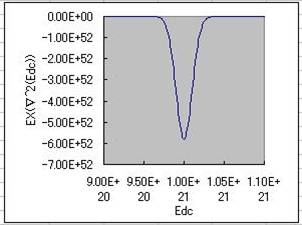
Where the absolute value of
E_DC is close to E1, the Laplacian of E_DC is large.
Its shape is same as a
normal distribution.
With this formula, I found
that the spherical solution that composed of radial electric field on the polar
coordinates.
A spherical steady solution of the non-linear wave equation
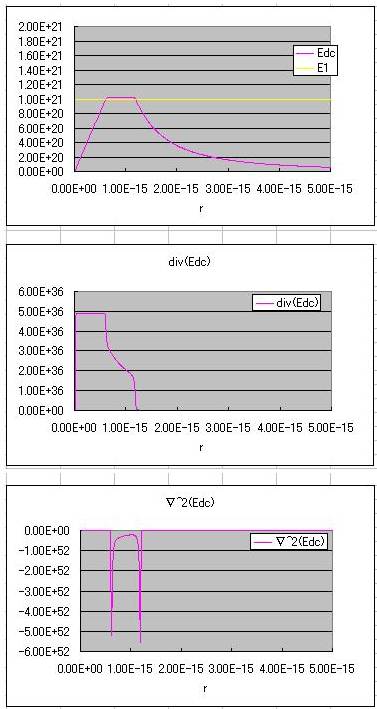
I searched the K1 constant
manually referring to the graph.
At large radius r, E( the
electric field) is close to the asymptotic curves from a point charge.
At radius r is small, so
that it reaches the E1 , and negative Laplacian E_DC.
Therefore E_DC bends. (Part of the right
shoulder).
Then E_DC becomes nearly
constant at slightly above E1.
When E_DC decreases then Laplacian
of E_DC increases.
This is a work of negative
feedback.
Once again E_DC bend when radius r is
smaller (the part of the left shoulder),
Then E_DC linearly
proportional to the radius r.
I call the right shoulder to
be "the outer shell",
and I call the the
left shoulder to be the inner shell"
A spherica vibrating solution
of non-linear wave equation
A possibility about explanation of
Bell's theorem
Relationship between
mass and speed of light pdf
A derivation of Klein–Gordon
equation from the standing wave
A derivation of Klein–Gordon
equation from the standing wave (1dimension)
A derivation of Schrödinger
equation from the standing wave
A reason why wave function is in
proportion to probability@ icontents
of reviewj
A derivation of
Dirac equation from standing waves
This solution is a combination of three 4 dimensional phenomena. And its
amplitude is constant.
So the number of dimensions is 3 ~ 4
- 1 = 11. In other words, it can be
said to be an 11-dimensional phenomenon.
Non-linear condition that
is consistent with the general theory of relativity