非線形波動方程式の定在波解
[振動数が質量に比例する条件]
量子力学より粒子の持つエネルギーは
![]()
ただしここでは![]() はエネルギー
はエネルギー ![]() はプランク定数
はプランク定数 ![]() は振動数
は振動数
特殊相対論より
![]()
ただし![]() は質量
は質量 ![]() は光速
は光速
以上より
![]()
となって質量は振動数に比例する。
「光速と質量の関係」[文献1]から質量は![]() の体積積分に比例すると推測できる。
の体積積分に比例すると推測できる。
もしも荷電粒子の固有振動数に共振した定在波が荷電粒子の周辺にあってその定在波の持つ![]() の体積積分が振動数に比例するような解があれば以上のことを説明できる可能性がある。
の体積積分が振動数に比例するような解があれば以上のことを説明できる可能性がある。
そこで次のような定在波解を考える。
![]() (1)
(1)
ただしこれ以降![]() は電界強度
は電界強度
![]() は
は![]() の関数
の関数
![]() は固有角周波数
は固有角周波数
![]() は一般に真空中の光速と呼ばれる定数
は一般に真空中の光速と呼ばれる定数
![]() を光速とし真空中で現在の測定精度以下の範囲で電界強度に依存して変化
を光速とし真空中で現在の測定精度以下の範囲で電界強度に依存して変化
するとし
![]() (2)
(2)
![]() (2a)
(2a)
とする。
ただし![]() ,
,![]() は定数
は定数
以下の波動方程式が適用できるとする。
![]() (3)
(3)
(1)と(3)左辺より
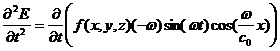
![]() (4)
(4)
(1)と (3)右辺より
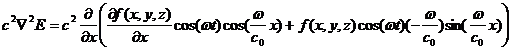
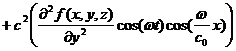
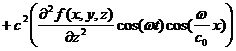
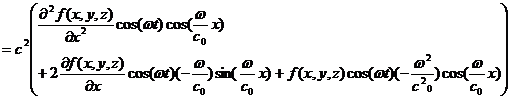
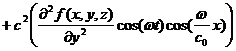
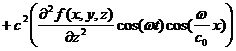
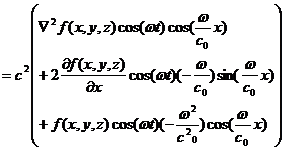 (5)
(5)
![]() と
と![]() についてフーリエ変換を行い
についてフーリエ変換を行い![]() 項を取りだすと
項を取りだすと
(4)式より
![]()
![]() (6)
(6)
(2)(5)式より
![]()
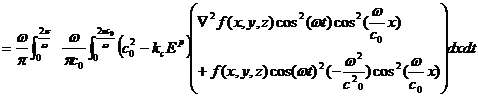
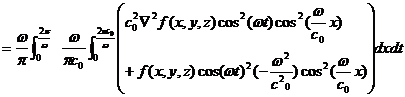
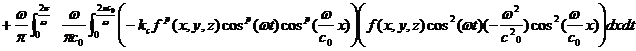
![]() (7)
(7)
したがって
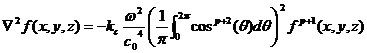 (8)
(8)
![]() を定数とし
を定数とし
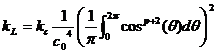 (9)
(9)
とすると(8)(9)より
![]() (10)
(10)
となって![]() のラプラシアンは振動数の2乗と
のラプラシアンは振動数の2乗と![]() の
の![]() 乗の積に比例する。
乗の積に比例する。
ここで極座標系において![]() を半径と角周波数で正規化できる条件を求める。
を半径と角周波数で正規化できる条件を求める。
![]() を基準半径とし
を基準半径とし
![]() (11)とする
(11)とする
![]() を正規化された半径とし
を正規化された半径とし
![]() (12)
(12)
![]() (13)とする。
(13)とする。
![]() と表現する。
と表現する。
![]() を正規化された
を正規化された![]() とし
とし
![]() (14)
(14)
とする。
![]()
![]() (15)
(15)
(10)(14)より
![]() (16)
(16)
(15)(16)より
![]() (17)
(17)
正規化ができるとすればこの式が![]() に依存しない条件として
に依存しない条件として
![]() (18)
(18)
が成立する必要がある。
したがって
![]() (18a)
(18a)
これが成立すると仮定すると(17)式を
![]() で割って
で割って
![]() (19)
(19)
となって![]() に依存しない正規化された式となる。
に依存しない正規化された式となる。
次に質量の総量を求める
(2)式をもう一度書くと
![]() (2)
(2)
![]() を
を![]() の平均とすると
の平均とすると
![]()
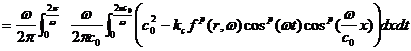
![]() (20)
(20)
![]() (20a)
(20a)
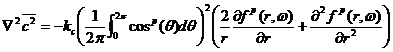
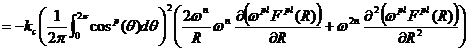
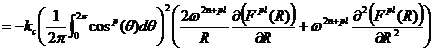 (21)
(21)
![]() を質量とし
を質量とし
「光速と質量の関係」[文献1]から
![]() (22)
(22)
とする
ただし![]() は微小体積
は微小体積
(21)(22)より
![]() (22a)
(22a)
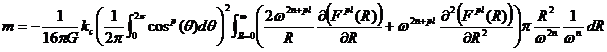
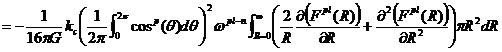 (23)
(23)
振動数が質量に比例するには
![]() (24)
(24)
が成立する必要がある。
これが成立すると仮定すると
![]() を振動数とし
を振動数とし
![]() (25)
(25)
ただし![]() を定数とし
を定数とし
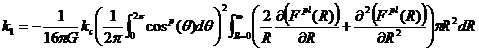 (26)
(26)
とする
条件をもう一度書くと
![]() (18a)
(18a)
![]() (24)
(24)
2つの式より
![]() (27)
(27)
![]() (28)
(28)
単純なケースとして![]() と
と![]() が正の整数である場合について検証してみること
が正の整数である場合について検証してみること
にする。
(9)(10)式より
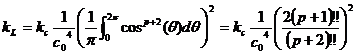 (29)
(29)
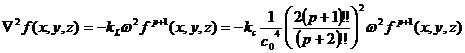
(29a)
(25)(26)式より
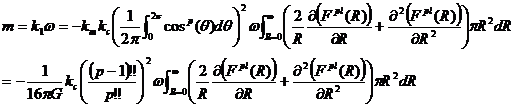 (30)
(30)
(28)より![]() が決定されれば
が決定されれば![]() が決定するので
が決定するので
|
|
|
|
|
|
|
|
|
|
|
となる。
ここで![]() の関数の形を検証してみる。
の関数の形を検証してみる。
(10)より
![]()
![]()
![]()
となることから中心の初期値から外に向かって積分することで![]() を求めることが出来る。
を求めることが出来る。
![]()
![]()
![]()
と仮の値を代入し差分法により![]() を求め横軸
を求め横軸![]() として両対数グラフにした。
として両対数グラフにした。
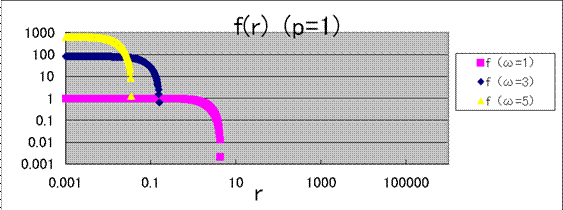
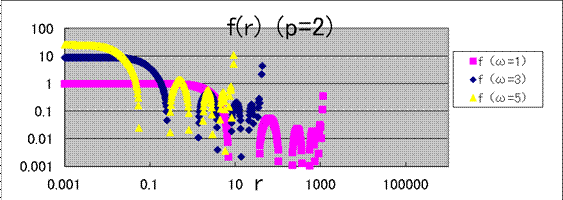
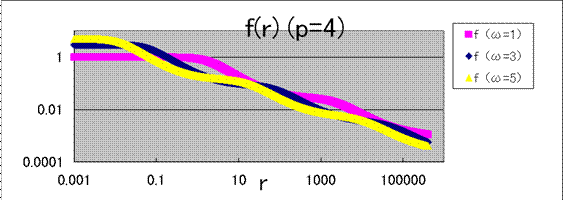
p=1, p=2では、rの増大とともに![]() は発散したがp=4では発散しなかった。
は発散したがp=4では発散しなかった。
![]() としp=4 ω=1の場合についてリニアスケールで関数の形を見てみると各値は収束している。
としp=4 ω=1の場合についてリニアスケールで関数の形を見てみると各値は収束している。
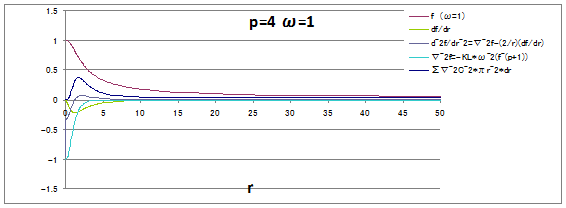
今後は![]() を重点的に検証することとする。
を重点的に検証することとする。
![]() (42a)
(42a)
(42a) (20a)より
![]()
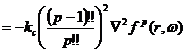
![]() (43)
(43)
(29a)より
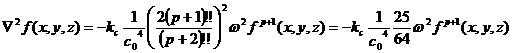
(44)
(30)より
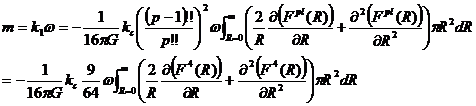
(45)
p=4について(42)よりF(R )を求めた。
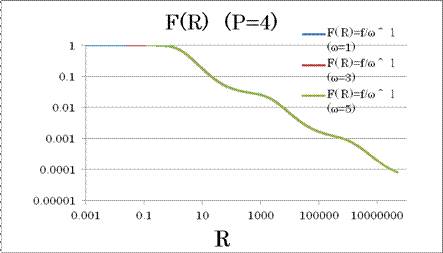
ωが変化してもF(R )は変化しないことが確認され、正常に正規化されることが確認
出来た。
(21) (22a)から質量mを求めた。
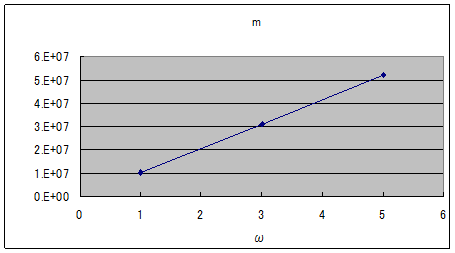
ωによって直線的に変化することから質量が振動数に比例することが確認できた。
これにより量子力学と相対論の本質的な繋がりを解明できる可能性がある。
参考文献
[1]長井鉄也「光速と質量の関係」
http://www.tegakinet.jp/wave/wave.files/lightweight.pdf